
However, elementary quantum mechanics requires that once one has the capability of obtaining which-path information, even in principle, the interference pattern must be suppressed, independent of whether one actually performs the measurement. However, as Bohr pointed out, one can imagine carrying out the same experiment with ( super) electrons of arbitrarily large charge, Ze, and indeed, for sufficiently large Z, one can determine which slit each electron went through.

In an experiment with ordinary electrons of charge e the uncertainty principle prevents measurement of the Coulomb field to the required accuracy, as we shall see below, following the prescription of Bohr and Rosenfeld for measuring electromagnetic fields ( 2, 3). Two-slit diffraction with single electrons, in which one measures the Coulomb field produced by the electrons at the far-away detector. Unlike for the electromagnetic field, Bohr's argument does not imply that the gravitational field must be quantized.
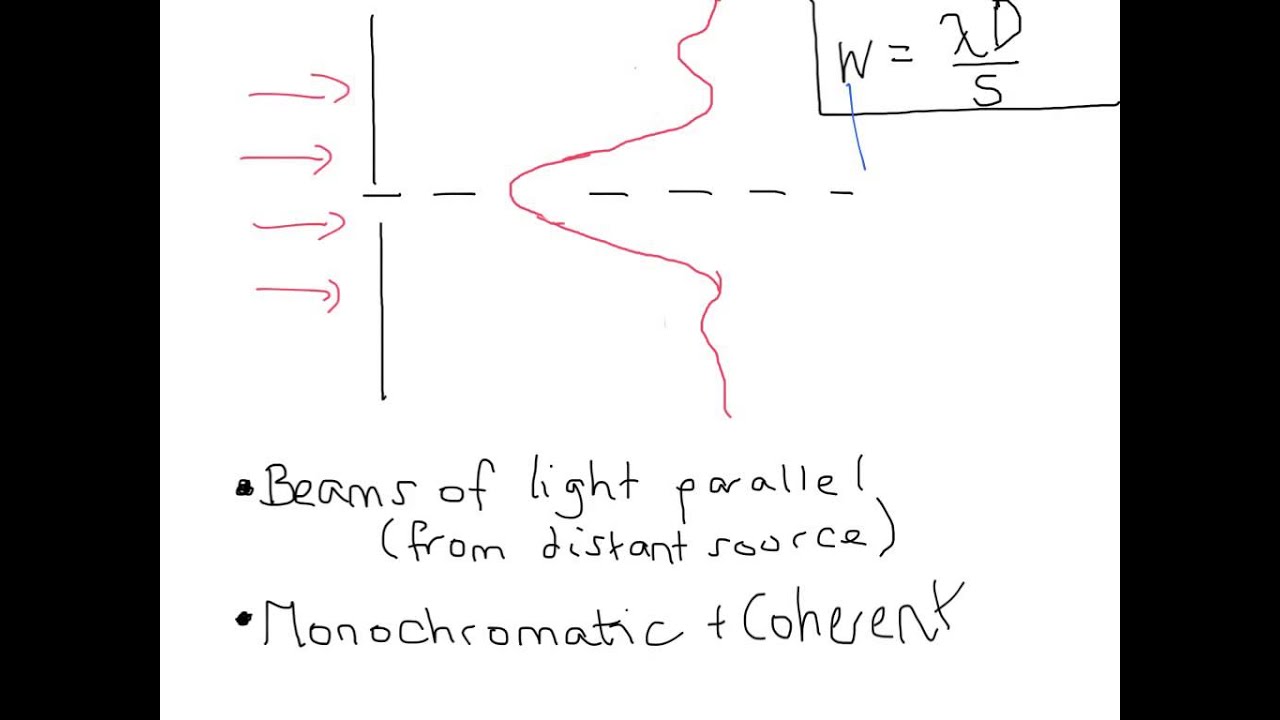
However, if one similarly tries to determine the path of a massive particle through an inferometer by measuring the Newtonian gravitational potential the particle produces, the interference pattern would have to be finer than the Planck length and thus indiscernible. Thus, the radiation field must be a quantized dynamical degree of freedom. The key is that, as the particle's trajectory is bent in diffraction by the slits, it must radiate and the radiation must carry away phase information. In the experiment a particle's path through the slits is determined by measuring the Coulomb field that it produces at large distances under these conditions the interference pattern must be suppressed. However, the particle-wave dynamics can not reproduce quantum mechanics in general, and we show that the single-particle statistics for our model in a double-slit experiment with an additional splitter plate differs qualitatively from that of quantum mechanics.We analyze Niels Bohr's proposed two-slit interference experiment with highly charged particles which argues that the consistency of elementary quantum mechanics requires that the electromagnetic field must be quantized. We show that the ensuing particle-wave dynamics can capture some characteristics of quantum mechanics such as orbital quantization. To understand theoretically the limitations of wave-driven particle systems as analogs to quantum mechanics, we introduce a Schrödinger equation with a source term originating from a localized particle that generates a wave while being simultaneously guided by it. To support our conclusions, we have carried out our own double-slit experiment, and our results, in particular the long and variable slit passage times of the droplets, cast strong doubt on the feasibility of the interference claimed by Couder and Fort.
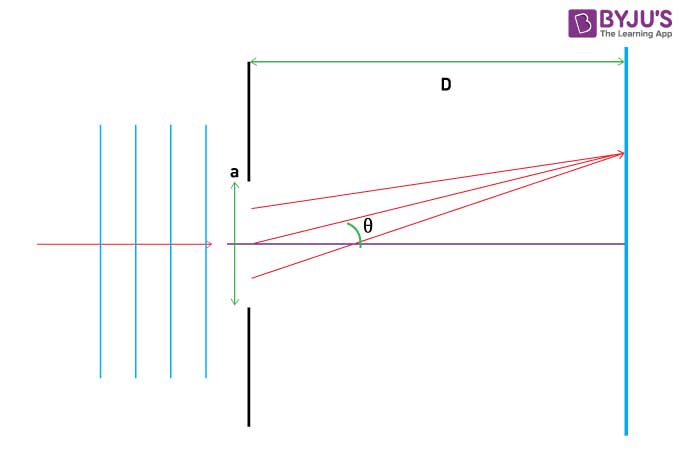
In the double-slit experiment with walking droplets, these relations are lost since one of the paths is singled out by the droplet. Quantum mechanical interference takes place between different classical paths with precise amplitude and phase relations. Here we argue, however, that the single-particle statistics in such an experiment will be fundamentally different from the single-particle statistics of quantum mechanics. In the experiment, an interference pattern in the single-particle statistics is found even though it is possible to determine unambiguously which slit the walking droplet passes. In a thought-provoking paper, Couder and Fort describe a version of the famous double-slit experiment performed with droplets bouncing on a vertically vibrated fluid surface.


 0 kommentar(er)
0 kommentar(er)
